Arguments related to a conjecture about the subgame perfect equilibria of a model of sequential location

author

introduction

The arguments here relate to my conjecture regarding the subgame perfect equilibria of a model of sequential location.

Without loss of generality, assume that F is uniform (so that, in particular, m = 1/2). The following observation is straightforward.

Lemma: In the outcome of every subgame perfect equilibrium each player who enters obtains the same fraction of the votes.

Proof: If every player does not receive the same fraction of votes, at least one player loses. This player can increase her payoff by staying out of the race.

n = 2

For the case of two players, the argument is very simple.

Proposition: For n = 2 the game has a unique subgame perfect equilibrium. The outcome of this equilibrium is that each player enters at m.

Proof

First consider the subgame following player 1's entry at a position other than m. In this subgame player 2 can enter and win outright, so that in every subgame perfect equilibrium of the subgame player 1 loses.

Now consider the subgame following player 1's entry at m. Player 2's best action in this subgame is to enter at m, leading the candidates to tie.

We conclude that the game has a unique subgame perfect equilibrium, in which each player enters at m.

n = 3

For the case of three players, the argument is a little more involved.

Proposition: For n = 3 the game has a unique subgame perfect equilibrium. The outcome of this equilibrium is that players 1 and 3 enter at m and player 2 stays out of the race.

Proof

First consider the subgame following player 1's entry at a position x₁ other than m. Without loss of generality, assume x₁ < m. Let

x₂ =	3/4 − x₁/2	if 1/6 ≤ x₁ < m
x₂ =	2/3	if 0 ≤ x₁ < 1/6.

(Note that 3/4 − x/2 = (1/2)[1/2 + 1 − x], the mean of 1/2 and 1 − x.) Given x₁ > 0, if player 2 enters at x₂ then (i) player 3 loses wherever she enters, and (ii) if player 3 stays out, player 2 wins outright (and, in particular, player 1 loses). Thus for x₁ > 0, in every subgame perfect equilibrium of the subgame player 2 enters and wins outright. For x₁ = 0, the unique subgame perfect equilibrium of the subgame entails player 2 and player 3's entering at 2/3, in which case all players tie.

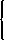
We conclude that in any subgame perfect equilibrium of the subgame following player 1's entry at a position different from m, she either loses or (if she enters at 0) ties for first place with players 2 and 3.

Now consider the subgame following player 1's entry at m. If player 2 enters at m, player 3 can win outright by entering close enough to m. If player 2 enters at a position different from m, player 3 can tie with player 1 for first place by entering at m. Thus in every subgame perfect equilibrium of the subgame, player 2 stays out.

If player 2 stays out, then player 3's best action is to enter at m.

We conclude that in every subgame perfect equilibrium of the subgame following player 1's entry at m, player 1 ties for first place (with player 3).

Putting the conclusions together yields the result.

n = 4

For the case of four players, I present here an argument that shows only that the game has a subgame perfect equilibrium of the conjectured form, not that it has no other subgame perfect equilibria.

Proposition: For n = 4 the game has a subgame perfect equilibrium in which players 1 and 4 enter at m and player 2 stays out of the race.

Proof

First consider the subgame following player 1's entry at m. I argue that in every subgame perfect equilibrium of this subgame, player 2 stays out. Suppose, to the contrary, that player 2 enters, say at x₂. Assume, without loss of generality, that x₂ ≤ m.

If x₂ = m, then for every position of player 3 there is a position of player 4 that wins outright, so that player 3 optimally stays out and player 4 consequently optimally enters at a position at which she wins outright, so that player 2 loses.
If 0 < x₂ < m, then if player 3 enters at 3/4 − x₂/2 (the mean of m and 1 − x₂), there is no position at which player 4 can win, and, in the absence of player 4, player 3 wins outright, so that player 2 loses.
If x₂ = 0, then if player 3 enters at 2/3, there is no position at which player 4 can win, and, in the absence of player 4, player 3 wins outright, so that player 2 loses.

Thus in every subgame perfect equilibrium of the subgame following player 1's entry at m, player 2 stays out. By the previous result, we conclude that in every subgame perfect equilibrium of the subgame following player 1's entry at m, player 3 stays out and player 4 enters at m.

The game has no subgame perfect equilibrium in which player 1 wins outright, because in any such equilibrium players 2 and 3 do not enter (by the Lemma), making it possible for player 4 to enter and win outright. Thus the game has a subgame perfect equilibrium in which player 1 enters at m, players 2 and 3 stay out, and player 4 enters at m.