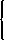X Y Z X
2,2 0,2 3,1 3,0 0,0 4,0 4,2 0,1 5,1 Y Z
- (5) Is any action of either player strictly dominated?
- (5) Is any action of either player weakly dominated?
- (5) Find the Nash equilibria of the game. Is any equilibrium strict?
X Y X
$5,$0 $50,$40 $10,$9 $80,$100 Y
Each player cares not about the amount of money she gets, but about the difference between the amount of money she gets and the amount of money the other player gets. (That is, she cares about the amount of money she gets minus the amount of money the other player gets.)
- (5) Model this situation as a strategic game.
- (5) Find the Nash equilibria.
- Players
- Two people.
- Actions
- Each person's set of actions is the set of nonnegative numbers.
- Preferences
- Person 1's preferences are represented by the payoff function
u1(a1, a2) = a1(2a2
and person 2's preferences are represented by the payoff function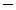 a1)
a1)u2(a1, a2) = a2(2
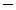 2a1
2a1 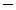 a2)
a2)
where P is the inverse demand function and Ci is firm i's cost function.i(q1, q2) = qiP(q1 + q2)
Ci(qi),
Find the Nash equilibrium (equilibria?) of the strategic game that models this situation when the inverse demand function is linear, given by
the cost function of firm 1 is C1(q1) = cq1, the cost function of firm 2 is C2(q2) = q22, and c < (3/4)
P(Q) =

Q
if Q 
0 if Q > ,
 .
.
(Carefully present the steps in your argument. Throughout your analysis, ignore the case in which the total output is so high that the price is zero--just assume that the price is always given by P(Q) = 
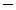 Q.)
Q.)
Specifically, the total demand facing firm i is the sum of Ri(pi) (the demand from i's regular customers) and the demand from customers who compare prices, which is the same as it is in Bertrand's model (D(pi) if pi < pj, (1/2)D(pi) if pi = pj, and 0 if pi > pj).
The functions R1, R2, and D are continuous and decreasing (a higher price reduces demand in each case), and R1(c) > 0, R2(c) > 0, and D(c) > 0. The cost function of firm i is defined by Ci(qi) = cqi for i = 1, 2.
- (5) Write down firm i's payoff function in the strategic game that models this situation.
- (5) Is the pair (c,c) of prices a Nash equilibrium?
- (10) Does the game have any (other?) Nash equilibrium (p,p) in which both firms charge the same price?