The topics in this Lesson present a bit more advanced material than was
built into the previous two Microeconomics Lessons. We begin with
indifference curve analysis. An indifference curve is presented in
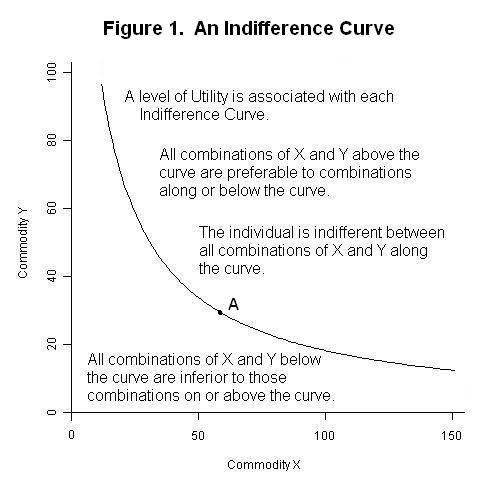
Figure 1 below.

Suppose we measure an individual's consumption of commodity X and commodity Y along the horizontal and vertical axes respectively and then arbitrarily pick a point in the resulting (X , Y) space such as, for example, point A. Now imagine that we label with a plus sign every point in the space that is preferred to point A and then label with a minus sign every point in the space that point A is preferred to. If we then draw a line that separates the plus from the minus signs, we will obtain the indifference curve shown in the above figure. The individual will be indifferent between all combinations of X and Y indicated by the curve and will prefer all combinations above the indifference curve to any combination on the curve. And any combination along the indifference curve will be preferred to all combinations below it.
Since every (X , Y) combination will have an indifference curve passing through it, we can add a third axis stretching upward from the bottom left corner of the figure measuring the degree to which the individual's preferences are satisfied, and visualize the infinitely many indifference curves as representing a smooth surface that rises as the consumption of commodities X and Y increase. We denote the degree to which preferences are satisfied as the level of utility and assume that individuals choose the combination of goods X and Y, among those available, that maximizes their utility, with an increase in utility occurring whenever there is an increase in the quantity of either X or Y consumed, holding consumption of the other good constant.
Utility theory thus assumes that individuals have an internally consistent set of preferences that do not change during the time-interval during which we are analyzing their behaviour. In this sense we assume that individuals are rational. Irrational behaviour is illustrated in Figure 2 below.
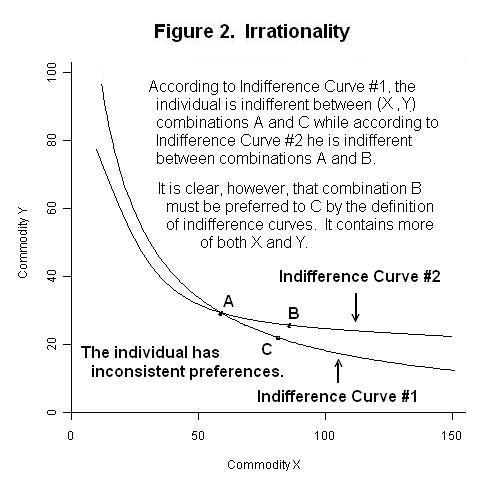
Suppose that an individual has indifference curves that cross, as in the case of Curve #1 and Curve #2 above. This implies that the individual is indifferent between combinations A and B and between combinations A and C. As a result, he must be also indifferent between points B and C. But point B has to be preferred to point C because it is above the indifference curve on which point C is located. The individual is consuming more of both goods at point B than at point C. The crossing of two indifference curves presents a logical contradiction in the sense that the individual is behaving inconsistently or, as we would say, irrationally.
Economists have often been criticized for their assumption that people are rational. After all, we can think of many examples of people doing stupid things. Irrational behaviour of friends and relatives and other people we observe is part of the human condition. In this respect, however, it is important to understand that economists' definition of rationality means simply that individuals behave consistently, however stupid and irrational that consistent behaviour might appear to others. And while it is clear that some peoples' behaviour may be unstable through time, the economist has to assume that the bulk of people whose behaviour is being analyzed have unchanged preferences during the period over which the analysis is taking place.
In fact, without an assumption that people have consistent preferences that do not change during the period being analyzed, no coherent analysis of social behaviour would be possible---all that would be possible is a factual delineation of what has happened in the past by historians who must carefully avoid any interpretation of those observed facts. Of course, psychologists and sociologists, and occasionally economists, will attempt to determine how and why preferences change through time, but they too have to assume coherent and internally consistent preferences that are capable of systematic interpretation.
In the simple case portrayed in the two Figures above, economists assume that an individual's utility can be expressed as a function of---that is, dependent on---the quantities of commodities X and Y consumed. Mathematically, we can write
1. U = U(X , Y)
where U is the level of utility and the function U(X , Y) states simply that the level of utility depends in some fashion on the levels of commodities X and Y consumed by the individual. If we want to get fancy and analyse a situation where the individual's preferences change, we could expand the utility function by inserting between the brackets an additional input, call it Z, that measures the forces causing preferences to change, yielding the function U(X , Y , Z). Analytical extensions of this sort are, of course, extremely difficult if not impossible to successfully pursue.
The presentation of the utility function in Equation 1 is extremely general---without additional specifications, the relationship denoted by U(X , Y) could take any form. Several important features of the utility function are always specified. First, as we noted above, increases in the levels of X and Y always lead to increases in U . That is, the partial derivatives of the utility function with respect to X and Y ---the changes in U associated with in small changes in each of X and Y holding the other constant---are positive. Mathematically, this imposes the two conditions
2. ∂U/∂X = ∂U(X , Y)/∂X > 0 and ∂U/∂Y = ∂U(X , Y)/∂Y > 0
where ∂U/∂X is the partial derivative of U(X , Y) with respect to X and ∂U/∂Y is the partial derivative with respect to Y. We refer to ∂U/∂X and ∂U/∂Y as, respectively, the marginal utility of X and the marginal utility of Y. Equations 2 specify that marginal utilities of X and Y are positive.
The second specified feature of the function U(X , Y) is the principle of diminishing marginal utility. This says that the marginal utility of X declines as the quantity of X increases and the marginal utility of Y declines as the quantity of Y increases. The slope of an indifference curve is the negative of the ratio of the marginal utility of X over the marginal utility of Y. To see this, imagine that the quantities of X and Y change by small amounts. The change in utility specified in Equation 1 can then be expressed mathematically as
3. dU = ∂U(X , Y)/∂X dX + ∂U(X , Y)/∂Y dY = ∂U/∂X dX + ∂U/∂Y dY
where the letter d preceding a variable denotes a small change in that variable. Since the level of utility must be constant---that is dU = 0 ---along an indifference curve, Equation 3 can be rearranged to yield
0 = ∂U/∂X dX + ∂U/∂Y dY
which can be further rearranged as
4. dY/dX = − ∂U/∂X / ∂U/∂Y
where dY/dX is the slope of the indifference curve. The principle of diminishing marginal utility implies that ∂U/∂X , the marginal utility of X, falls as the quantity of X consumed increases and that ∂U/∂Y , the marginal utility of Y, rises as the quantity of Y consumed decreases. As can be seen from Equation 4, this implies that the indifference curve gets flatter as the quantity of X consumed increases relative to the quantity of Y consumed. Or, as we say, indifference curves are concave outward, or convex with respect to the origin. The slope of the indifference curve is called the marginal rate of substitution, which declines as the quantity of X increases relative to the quantity of Y.
Of course, the amounts of commodities X and Y that the individual will be able to consume depends on the level of that person's income. If the entire income is spent on commodity X, the maximum quantity that can be consumed is given by the distance between the origin and point B on the horizontal axis of Figure 3 below. If the entire income is spent on commodity Y, the maximum quantity that can be consumed is given by the vertical distance between the origin and point A. If the prices of the two commodities facing the individual are constant, the ratio of the price of commodity X to the price of commodity Y is given by the slope of the budget line running from point A to point B.
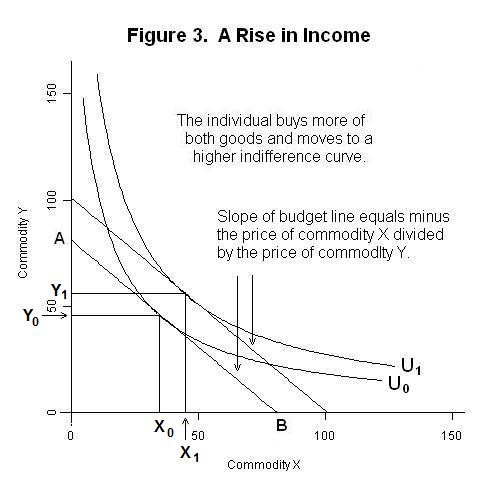
The optimal quantities consumed will be that combination of X and Y that puts the individual on the highest possible indifference curve---that is, quantities X0 and Y0 on the above Figure. Note that the equilibrium quantities are those for which the slope of the indifference curve equals the slope of the budget line---that is, where the marginal rate of substitution equals the price ratio.
Now suppose that the level of the individual's income increases without any change in prices. More of both commodities can now be consumed and the price ratio does not change, so the budget line shifts outward with the new budget line being parallel to the original one. The level of utility increases from U0 to U1 and the individual's consumption of the two goods increases to X1 and Y1 . At this point we must keep in mind that the indifference map in Figure 3 assumes that both X and Y are normal goods---that is, that indifference curve U1 is tangent to the new higher budget line at a point to the right of output level X0. In the case where X is an inferior good, this tangency would be to the left of output level X0 and the quantity demanded of commodity X would decline as a result of the increase in income.
Finally, let us suppose that the price of commodity X falls, with no change in money income. The results are shown in Figure 4 below.
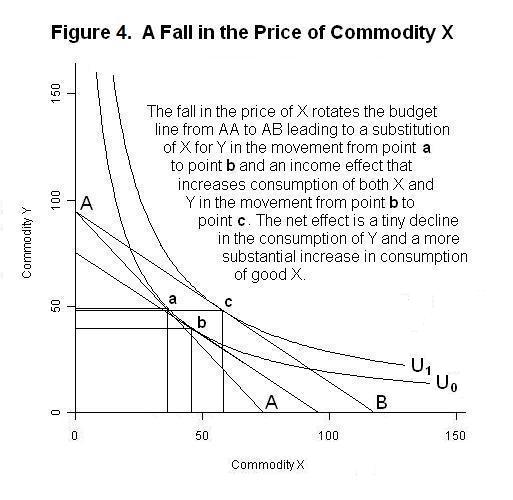
If the individual were to spend his entire income on commodity X, the amount of X purchased would now be higher. Since the price of good Y has not changed, neither has the maximum possible consumption of that commodity. The fall in the price of X has thus reduced the slope of the individual's budget line by rotating it counter-clockwise around point A on the vertical axis. The new utility maximum occurs at point c with a big increase in the quantity of good X consumed and a slight decline in consumption of good Y.
It is important to distinguish between two components of the shift from the initial equilibrium point to the final equilibrium at point c---the income effect and the substitution effect. The decline in the price of X leads to a substitution of good X for good Y along the initial indifference curve, holding real income---that is utility---constant. This substitution effect is indicated by the movement from combination a to combination b along indifference curve U0. The fact that real income has increased as a result of the decline in the price of good X, holding nominal income and the price of good Y constant, results in an increase in the quantities consumed of both goods, represented by the movement from combination b to combination c. This income effect is represented by the movement from indifference curve U0 to U1. As you can see from the above Figure, the quantity consumed of good X increases as a result of both the substitution and income effects while the quantity of good Y consumed declines as a result of the substitution effect and increases by slightly less than that amount as a result of the income effect, leaving a slight overall decline.
It should now be clear why demand curves slope downward when the goods, as in the above analysis, are substitutes for each other. It is obvious from Figure 4 that a fall in the price of commodity X, holding nominal income constant, results in an increase in the demand for that good. In that Figure, the fall in the price of good X also shifts the demand curve for good Y slightly to the left because the substitution effect more than offsets the effect of the decline in real income. Also, it is clear from Figure 3 that an increase in nominal income, holding prices constant, shifts the demand curves of both goods to the right and, therefore, that both commodities in that example are superior goods.
In the real world, each individual will spend her income on many goods in each period of her life, and will face relative prices that may change from period to period along with the interest rate, which measures the cost of consuming in the present as opposed to future periods. In a world where consumption externalities are present, she may also experience gains and losses in utility from the behaviour of others over which she has no control. This means that more advanced analysis will involve a utility function with many more arguments. On the basis of our two-commodity analysis above, however, it is reasonable to expect that the marginal rate of substitution of each good for each other in the utility function will, in equilibrium, equal the relative price of that pair of goods. The principles of diminishing marginal utility and diminishing marginal rate of substitution can reasonably be assumed to be widely applicable.
It is now time for a test. As always, think up your own answers before looking at the ones provided.
Question 1
Question 2
Question 3
Choose Another Topic in the Lesson