The exchange rate has an important relationship to the price
level because it represents a link between domestic prices and
foreign prices. For example, ignoring taxes, subsidies and shipping
costs, the price of wheat in Canada must equal the exchange
rate (price of the U.S. dollar in terms of the Canadian dollar)
times the U.S. dollar price of wheat. For a commodity, call it
x , that is traded internationally, we can thus write
1.
Px = Π P*x
where Px is the domestic price (in domestic currency),
P*x is the price abroad (in foreign currency) and
Π is the exchange rate (price of foreign currency in units
of domestic currency). This relationship is called the law of one
price.
If every good produced in the domestic economy is also produced
in the foreign economy, and if the shares of each good in aggregate
output are the same in both economies, then the domestic price level
will equal the exchange rate times the foreign price level.
2.
P = Π P*
where P and P* are the domestic and foreign price
levels. It follows, then, that if there is inflation in the domestic economy,
not matched by inflation abroad, so that P rises relative
to P*, the exchange rate Π (domestic currency
price of foreign currency) has to rise---that is, the domestic currency must
depreciate in terms of foreign currency.
Suppose that the government decides to fix the price of its
currency in terms of some foreign currency---that is, adopt a
fixed exchange rate. In this case, Π in Equation 2
will be fixed at some level, say, Π0. If the price
level in the foreign country happens to P*0, the
domestic price level will be fixed at
3.
P0 = Π0 P*0.
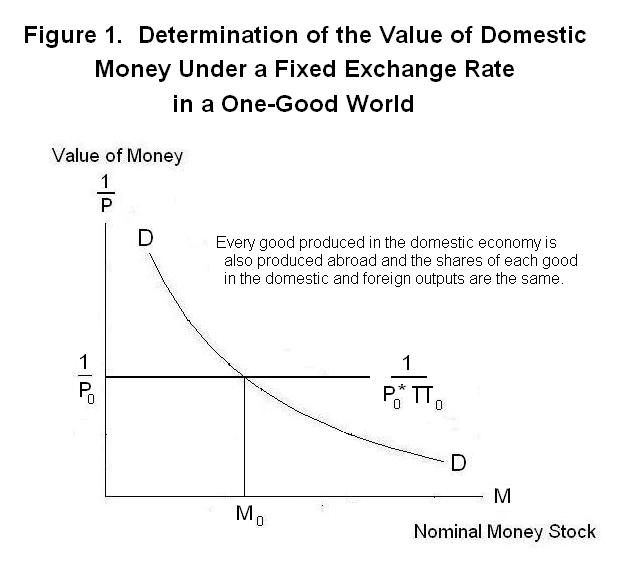
As we can see from Figure 1, this will require that the domestic
money supply be fixed at M0.
By fixing the exchange rate, the domestic authorities tie their
hands with respect to monetary policy---they are forced to create a
specific equilibrium nominal money supply. As a matter of policy,
the government can control either the domestic money supply or the
country's exchange rate but not both.
At this point we must recognize that the economy we are
analyzing is part of a larger world and examine the relationship
between the price level and the exchange rate. The exchange rate
is the price of foreign money in units of domestic money or, under
an alternative definition, the price or value of domestic money in
units of foreign money. It is of fundamental importance because every
time domestic residents want to buy something abroad they must
exchange domestic currency for foreign currency, and every time
foreigners want to buy domestic goods they must exchange foreign
currency for domestic currency.

When the government fixes the exchange rate, it invokes a natural mechanism that keeps the domestic money supply at its equilibrium level. In order to fix the exchange rate, the government must stand ready to purchase or sell domestic currency for foreign currency at its announced price. If the domestic money supply is too high, people will spend the excess abroad, buying foreign currency with home money to enable those purchases. This will cause the price of foreign currency in terms of domestic currency to be bid up. To maintain the exchange rate at the official level, the government has to sell foreign currency for domestic currency, taking home money out of circulation in the process. For the purpose of doing this, it keeps reserves of foreign currency on hand---the country's stock of foreign exchange reserves.
If the domestic money supply is too low, the opposite will happen. Too much will be sold abroad and people will be exchanging too much foreign currency for domestic currency. The government has to buy foreign currency to keep the price of foreign currency in terms of domestic currency from falling below the official level. This increases the country's stock of foreign exchange reserves and puts additional domestic money in circulation.
The government can choose, of course, to not purchase and sell foreign currency for domestic currency when there are excess sales or purchases by domestic residents abroad. In this case, Π will adjust to reflect the different domestic and foreign rates of money growth and inflation---there will be a flexible exchange rate.
In the analysis in the other Topics in this Lesson, we always assume flexible exchange rates. This enables us to think about domestic money and prices without worrying about what is happening in the rest of the world. We will be four Lessons further along in the sequence before we look again at exchange rates, and a full understanding of how they are determined and their relationship to domestic economic policy will only emerge with completion of the entire sequence of Lessons. Nevertheless, before concluding this present Lesson we need to discuss further the law of one price and the relationship between the domestic and foreign price levels.
In order to write down Equation 2 we had to assume that all goods are produced everywhere and can be freely bought and sold across international boundaries without the impediment of transport costs, tariffs, taxes, or subsidies, so that Equation 1, the law of one price, holds for every good. Then we also assumed that each good represents the same fraction of aggregate output in each country so that countries' price indexes (which are assumed to be output-weighted averages of the prices of goods produced) are the same when the currencies exchange for each other on a one-for-one basis.
Of course, none of these assumptions are true, so how does the analysis change when they are false? Transport costs, taxes, tariffs and subsidies are not a problem because we can think of prices as being net of these distortions. But many goods are not traded internationally. The classic example is haircuts---one can obtain a haircut for, perhaps, 50 cents in India but the costs of flying there to obtain it are prohibitive. Since people cannot migrate freely between countries, the labour share of production represents a non-traded component of every good. This is why the price of a McDonalds hamburger, when measured in U.S. dollars, is not the same in all countries. Sides of beef and wheat flour can be purchased at roughly the same real price everywhere, but the labour used to make the patties, bake the bread, and provide the transport, cooking and clerical services is cheaper some places than others. Buildings, too, are built with local labour.
For these reasons a unit of aggregate output will not have the same price in all countries when measured in a single currency. The ratio of a country's price level to the price level in the rest of the world when all prices are converted into the same currency is called the country's real exchange rate. It is the relative price of domestic output in terms of foreign output and can be written as
4. Q = P /(Π P*).
where Q is the real exchange rate and the other variables are as previously defined.
It is obvious that each country's real exchange rate will depend on which goods it produces (not every good is produced in all countries), how highly those goods are valued in world markets and on how high the productivity of domestic labour (in producing domestic aggregate output) is relative to the productivity of foreign labour (in producing rest-of-world aggregate output). The respective productivities of labour will determine the real costs of producing non-traded goods at home relative to abroad. In a world where technological change is occurring and all countries are not equally endowed with natural resources, it is unreasonable to expect that any country's real exchange rate will be constant through time. The view that equilibrium real exchange rates are constant over time is called the purchasing power parity theory and it is now well-known that this theory does not hold.
Nevertheless our argument that governments lose control over their money supplies when they fix the nominal exchange rate holds regardless of what determines countries' real exchange rates. Given the definition of the real exchange rate in Equation 4, the domestic price level must equal
5. P = Π P* Q.
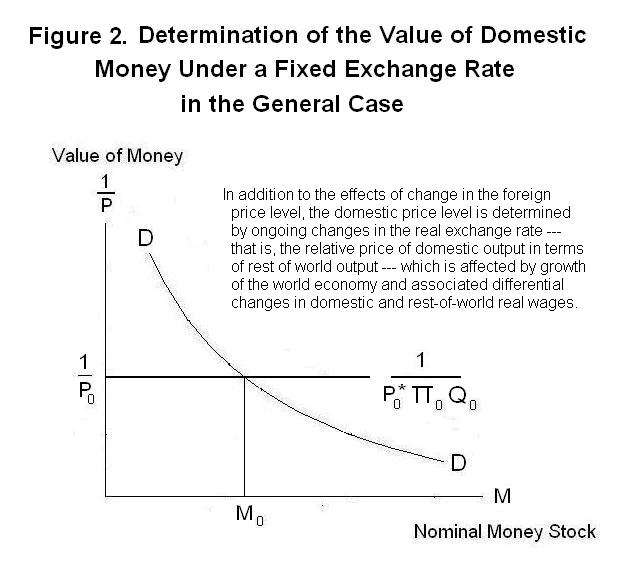
If the government fixes Π, then P will be determined by the current levels of P* and Q as shown in Figure 2. The money supply must be maintained at some level such as M0. Moreover, changes in Q as a result of technological change both at home and in the rest of the world will lead to changes in P that are beyond the control of domestic monetary policy. To maintain control over the domestic price level, the government must adopt a flexible exchange rate. The nominal exchange rate will then be determined by the degree of domestic relative to foreign inflation and the movements in Q that occur as the domestic and rest-of-world economies grow through time.
When conflicting domestic political forces make it impossible for the government to control the money supply it may be possible for the majority of voters to agree on a commitment to fix the price of the domestic currency in terms of the currency of some low-inflation country like the U.S. Fixing the exchange rate in this way takes control of the domestic money supply away from the domestic government and ties the domestic price level to that of the foreign country. Argentina in fact did this a number of years ago to successfully deal for a while with its perennial problem of high inflation
It is now time for a test. As always, think up your own answers before looking at the ones provided.
Question 1
Question 2
Question 3
Choose Another Topic in the Lesson