The efficiency wage theory arises from the observation that
workers will work harder when firms pay them wages in excess of
market levels. If all firms pay above-market wages and refuse to
hire workers for less, wage rates in the economy will be above
the market-clearing level and unemployment will result.
But why would firms not reduce wages, and workers agree to
work efficiently at these lower wages, when there is unemployment
in the economy? The reason why firms fix the wage rate independently of the
reservation wages of workers stems from the assumed production
function:
1. Y
= F(e(w) n)
where Y is output, e(w) is effort per worker as
a function of the real wage rate w, and n is the
quantity of labour employed. Notice
that e(w) n represents total effort---effort per worker (or per
hour) times the number of workers (or hours worked)---and is the
single variable input in the production function, capital being
present in the background but constant.
To maximize its profits the firm must maximize the excess of the value of
output over the variable cost of producing it, the fixed cost of
employing capital being constant. This profit function can be
written
2. x
= F(e(w) n) - w n
where x is the excess of revenue over variable cost.
To maximize its profits the firm must choose the levels of w
and n for which x is a maximum---these levels will
be those for which the changes in x resulting from small changes
in either w or n will be zero.
Taking the change in x resulting from a small change
in n (that is, the partial derivative of x with respect
to n) and setting it equal to zero, we obtain
3.
F′(e(w) n) e(w) - w = 0
where F′(e(w) n) is the change in output with respect to a
small change in total effort---that is, the derivative of F with
respect to e(w) n . This implies
4.
F′(e(w) n) = w / e(w)
The firm must employ additional labour up to the point where the
marginal product with respect to effort equals the real wage rate
per unit of effort.
Taking now the change in x resulting from a small change in
w ---that is, the partial derivative of x with respect
to w ---and setting it equal to zero, we obtain
5.
F′(e(w) n) n e′(w) - n = 0
where e′(w) is the marginal response of effort to the
wage rate or, in mathematical terms, the derivative of e(w) with
respect to w. Dividing both sides by n and rearranging
the terms, we can convert this expression into
6.
F′(e(w) n) e′(w) = 1 .
To maximize profits, the wage rate must be adjusted until the
marginal product of effort times the marginal response of effort
to the real wage rate equals unity.
Profit maximization requires, of course, that both Equation 4 and
Equation 6 hold simultaneously. Substituting Equation 4 into
Equation 6 to eliminate F′(e(w) n), we obtain
7.
w e′(w) / e(w) = 1 .
This equation says that to maximize its profit the firm must pay
that real wage for which the elasticity of effort with respect to
the wage rate equals unity---that is, where
(Δe/Δw)(w/e) =
(Δe/e) / (Δw/w) = 1
with Δ signifying a small change in the variable that
follows. This is called the
Solow Condition after Nobel Prize winning economist Robert
Solow (1924- ). The important thing to notice about this equation is
that the quantity of labour employed n does not appear in it.
The real wage rate is set independently of the level of employment.
Then the latter is obtained by substituting this equilibrium value
of w into Equation 4.
The basis for the Solow Condition can be seen intuitively.
For any initial number of workers hired, it always pays the firm
to increase the wage rate if the resultant percentage increase in
effort exceeds the percentage increase in the wage---this will mean
that effort per dollar spent is increasing or, alternatively, that
cost per unit of effort is falling. Any given level of output can
then be produced with fewer workers and at lower cost. On the other
hand, if the resulting percentage increase in the level of effort is
less than the percentage increase in the real wage it will pay the
firm to reduce the wage, the reduction in labour cost being greater
than the decline in the value of output produced.
Accordingly, the firm will set the wage rate at that level for
which a tiny percentage increase in the real wage will induce an
equal percentage increase in worker-effort. Thus, in equilibrium,
Δe/e = Δw/w
which, of course, implies
(Δe/Δw)(w/e) = 1
as noted above.
After choosing the wage rate for which this Solow condition holds,
the firm will choose the number of workers for which the marginal
value of output produced will equal the real wage rate. The wage
rate will be set independently of the level of employment although
the level of employment subsequently chosen will depend on the real
wage rate.
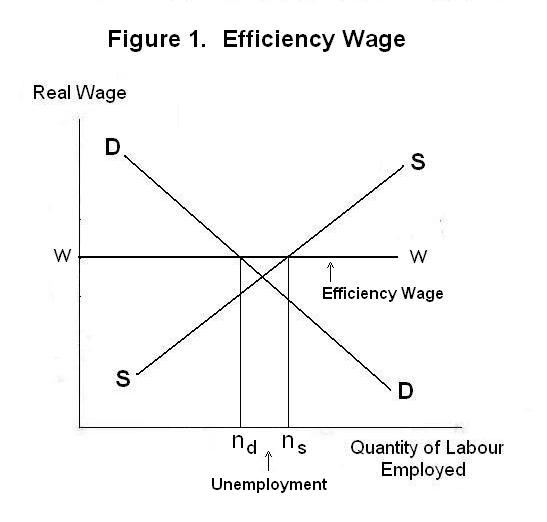
An important implication of this can be seen with reference
to Figure 1. The line ww gives the wage rate set by firms
according to the Solow condition. At that profit maximizing wage rate the
optimal level of employment of labour by firms happens to
be nd units. The quantity of labour time workers
wish to supply at that wage rate is ns. There is an
equilibrium level of unemployment in the economy
of (ns - nd). Although there
is no reason why the optimal quantity of labour demanded by firms at the
profit maximizing wage need be less than workers are willing to supply, there
is nothing to rule that out. The model implies that there could
easily be permanent unemployment.
We end this Lesson with a brief review of two other theories
of wage rigidity. First we will examine Efficiency Wage
theories and then we will turn to the role of insiders and
outsiders in wage determination. Efficiency wage theories can
be traced back at least to the work of Harvey Leibenstein (1922-1994) in
the 1960s and Joseph Stiglitz (1943- ) in the 1970s.
The Insider-Outsider theory is due to research by Assar
Lindbeck (1930- ) and Dennis Snower (1950- ).

This seemingly pathbreaking result follows, however, from two very restrictive assumptions of the model. First, the function e(w) relating effort to the wage rate is defined independently of socioeconomic conditions. Do workers in, say, Namibia have the same e(w) function as U.S. workers? If not, what determines e(w)? If worker-effort depends on economic conditions, why would workers choose wage-effort combinations that leave them permanently unemployed? Second, the assumption that all that matters in production is total labour effort, regardless of the number of units of labour generating that effort, is also very restrictive. Since, to take an example, only one person can drive a bus or truck at any time, it is impossible to separate the total quantity of driving services from the number of people doing the driving. And two computer programmers each giving half-effort will surely not always produce the same amount of usable code as one competent programmer.
Moreover, in many industries in an economy, firms can monitor worker effort and make explicit or implicit contracts with workers to each deliver a specific quantity of effort at a specific wage. This would mean that wages would be set along a quality-of-work adjusted labour supply curve as shown in Figure 2, reflecting the quantity of quality-adjusted labour services delivered. And any given quantity of labour services indicated along the curve will be associated with a particular number of workers who happen to be supplying those services. The intersection of this supply curve with the demand curve for labour will give the equilibrium level of employment. Anyone who wishes to supply labour services at the wage offered per unit of service can obtain employment.
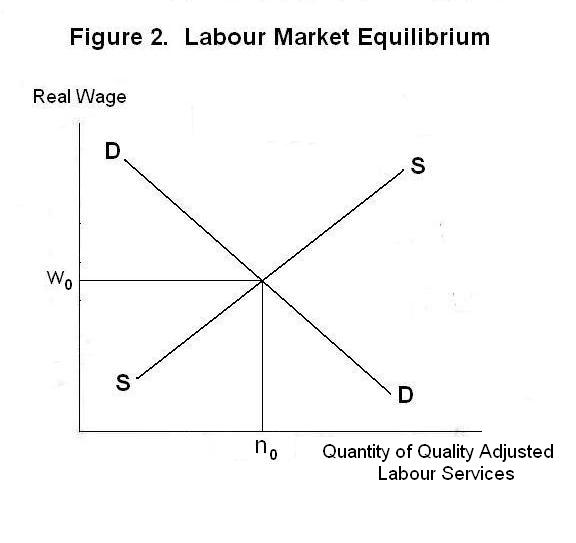
Some firms will find it profitable to pay higher-than-average wages and demand correspondingly higher-than-average effort. This will enable them to select workers of above-average quality. Other firms will find it profitable to operate with lower-quality labour. At worst, the efficiency-wage model in Figure 1 would apply only to certain industries in any economy. If fewer workers obtain jobs in those industries than want to work at the wages offered, the displaced workers will go to other industries and bid down wages there. Aggregate unemployment thus need not occur and Figure 2 will remain an adequate representation of the market for labour in the economy as a whole.
Like efficiency wages, insider-outsider theories can give useful insights into employment in particular firms and industries but provide little basis for economy-wide unemployment. In our analysis of contract theories in Topic four of this Lesson we noted that it is in the interest of firms to guarantee wage and employment stability to senior workers. Workers will accept lower wages in return for job security. It is also the case that currently employed workers are worth more to a firm at any given wage than new hires without in-firm experience. This is because the firm has had an opportunity to evaluate and train its current employees and to weed out those who lacked sufficient competence.
Given that workers currently inside the firm are worth more to it than those outside, they can attempt to capture these rents by demanding benefits in excess of the wage that would be paid to new hires from the outside. They can demand higher wages and restrict employment to equivalently raise their marginal products by refusing to work cooperatively with new workers hired from the outside. According to the insider-outsider theory, this will cause wages offered by the firm to be permanently above the market-clearing level---there will be workers willing to work at the going wage that the firm will refuse to hire. Generalized across the whole economy, this will result in the labour market situation illustrated by Figure 3. There will be permanent unemployment.
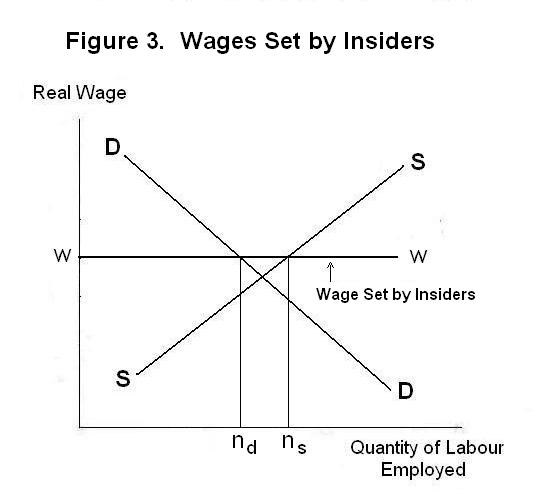
The problem with this theory is that, while it could easily apply to specific firms and industries in an economy, it is hard to imagine that every sector of the economy can be represented in this fashion. In many occupations, especially those requiring little skill, the competence of a worker can be evaluated very quickly and established workers can be rewarded by a small raise after a short time on the job. To the extent that there are industries to which the insider-outsider theory does not apply, workers banned from elswhere by insiders will simply bid down wages in these industries. Although there will be more people willing to work in industries dominated by insiders than jobs provided, everyone who wants a job will be able to find one somewhere in the economy.
The notion of insiders vs. outsiders can be extended to the political sphere. Workers having political influence, usually the high-skilled workers, can be thought of as insiders who are able to lobby governments for policies that discriminate in their favour against less skilled and influential workers, the outsiders. One example of this is pressures by skilled workers for minimum wage legislation. To the extent that, say, two unskilled workers can do the work of one skilled worker, a minimum wage above the going wage of unskilled workers will price them out of the labour market, increasing the demand for and wages of skilled workers.
Another example is the concern by affluent wage-earners in the developed industrial countries over the use of child labour in less developed countries. A law preventing importation of goods produced with child labour deprives children in poor countries of their best opportunity to earn income, forcing them onto the street to beg and shine tourists' shoes. At the same time, the elimination of competition from cheap foreign goods raises wages of skilled workers in advanced countries.
Of course, government policies that create aggregate unemployment cannot be blamed entirely on the political activities of insiders in the labour market. Many well-meaning but misinformed people support such policies.
It is time for a test. Make sure you hink up your own answers before looking at the ones provided.
Question 1
Question 2
Question 3
Choose Another Topic in the Lesson