It is now time to develop some technical concepts that will
be useful in later analysis. The first of these is the concept
of elasticity. Until now we have described the shapes of demand
and supply curves in terms of their slopes. It is not always
meaningful to describe curves as flat or steep, because whether
a curve appears flat or steep depends upon the units in which
price and quantity are measured.
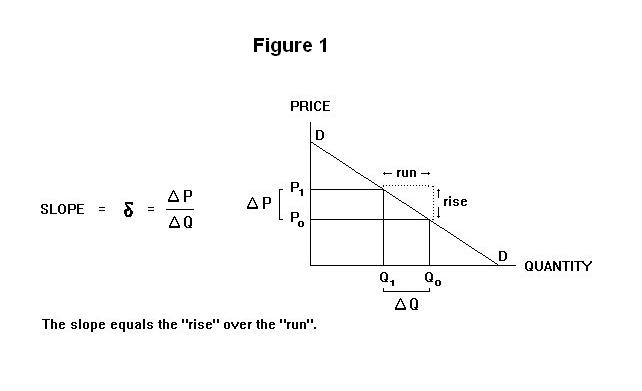
The slope of the demand curve is shown in Figure 1. Let Δ
represent the words "small change". We can then express the
slope of the demand curve, denoted by the greek symbol δ, as
1.
δ = ΔP /ΔQ
Measure the quantity of eggs in dozens and the price of eggs
in dollars. If, say, a rise in price of $1.00 reduces egg consumption
by 5 dozen as we move up along the demand curve, the slope will be -0.2.

Now suppose that we measure the quantity in numbers of eggs and the price in dollars as before. The same demand curve will now be flatter---a rise in the price of $1.00 will reduce egg consumption by 60 eggs, yielding a slope equal to -0.016667. If, alternatively, we were to measure the price of eggs in cents and the quantity of eggs in dozens, the slope of this same demand curve would then be -100/5 = -20. The apparent slope of the line on the graph will depend as well on how widely we space the units of price and quantity along the axes---if, for example, the quantity units are spaced a quarter of an inch apart the curve will appear steeper than if they are spaced half an inch apart.
By measuring the responsiveness of quantity to changes in price using the concept of elasticity, we avoid this dependence on units of measurement. The elasticity of demand is defined as the relative change (or percentage change) in quantity divided by the relative (or percentage) change in price. Let us use the greek symbol Φ to denote the elasticity of demand. Then we can write
2. Φ = ( ΔQ / Q ) / ( ΔP / P )
Since dividing by a number is equivalent to multiplying by its reciprocal we can rewrite the above equation as
3. Φ = ( ΔQ / Q ) ( P / ΔP ) = ( ΔQ / ΔP ) ( P / Q )
Since the slope of the demand curve is equal to the change in price divided by the change in quantity, the term ( ΔQ / ΔP ) in the above equation is the reciprocal of the slope. Then we can write Equation 3 as
4. Φ = ( ΔQ / ΔP )( P / Q ) = ( 1 / δ )( P / Q )
The elasticity is the reciprocal of the slope multiplied by the ratio of price over quantity. All this is illustrated in Figure 2 where the elasticity of demand is measured relative to the initial price-quantity combination ( P0,Q0 ) . It turns out that the elasticity will not be constant as we move along the curve. As should be clear from Equation 4, given a constant slope, the elasticity will decline as P / Q declines as we move down to the right along the straight-line demand curve---at the vertical axis where Q is zero the elasticity is infinite and at the quantity axis where P is zero the elasticity is zero.
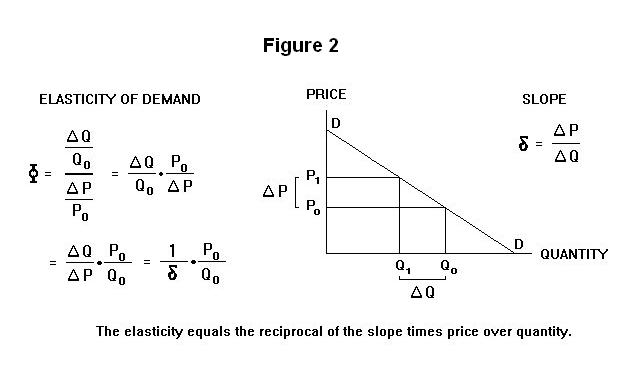
As shown in Figure 3 below, the elasticity of supply is calculated in exactly the same way as the elasticity of demand---the only difference is that the elasticity of supply is positive while the elasticity of demand is negative, reflecting the fact that the supply curve is upward sloping and the demand curve negatively sloped. We denote the slope of the supply curve by θ in the figure and measure the elasticity relative to the initial price-quantity combination ( P0 , Q0 ) . The elasticity will not be constant as we move up along a straight-line supply curve unless that line passes through the origin, in which case both the slope and the ratio P / Q will be constant.
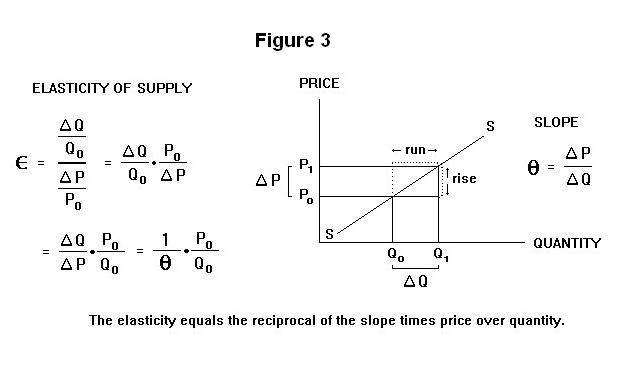
The total revenue to the seller of a commodity, or total expenditure by the purchaser, is obtained by multiplying the price by the quantity. It appears in Figure 4 as the area of a rectangle whose bottom left corner is the origin and top right corner is a point on the demand curve. The top left and bottom right corners equal price and quantity respectively. The shaded rectangle in Figure 4, for example, gives the total revenue at point c on the demand curve---the product of the price P0 and the quantity Q0. The total revenue at point a is the rectangle P1 a Q1 0.
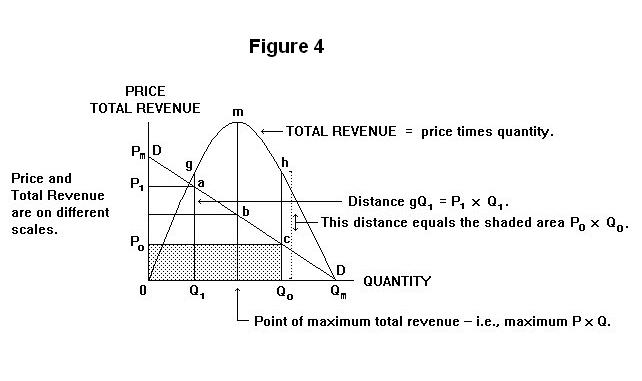
It is also clear in the above Figure that the total revenue varies as we move along the demand curve. The total revenue at zero quantity and price Pm is zero. As we move down along the demand curve, the total revenue increases, reaching its maximum at the point b (which is middle-distant from the two ends of the curve) and then declines, reaching zero again at price zero and quantity Qm.
Total revenue is portrayed in the Figure as the inverted parabola 0 g m h Qm ---it is measured on a different scale on the vertical axis, of course, than is the price. The shaded area P0 c Q0 0 is equal to the distance h Q0. Similarly, the area of the rectangle under the demand curve at point b equals the perpendicular distance between m and the horizontal axis. And the area of the rectangle under the demand curve at point a equals the distance g Q1.
Marginal revenue is defined as the change in total revenue that occurs when we change the quantity by one unit. We can express the marginal revenue, denoted by MR, as
5. MR = ΔTR / ΔQ
where TR is total revenue. The marginal revenue is thus the slope of the total revenue curve in Figure 5. At quantity zero, the marginal revenue is equal to the price---selling the first unit adds one times the price of that unit to the total revenue. As quantity increases the marginal revenue falls because as we add successive units not only is the price of the last unit lower than the price of the previous unit but all previous units have to be sold at this lower price.
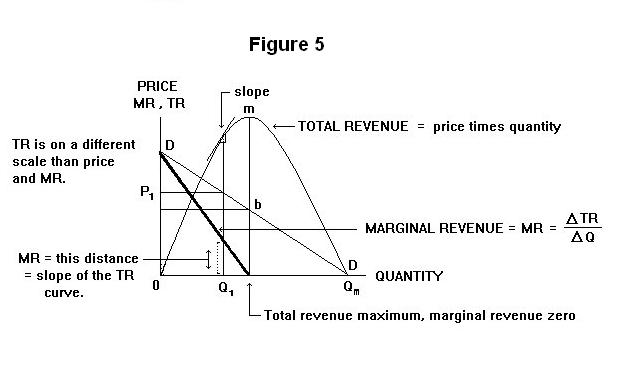
Marginal revenue for each quantity sold is given in Figure 5 as the distance between the thick line and the horizontal axis at that quantity. This distance is equal to the slope of the total revenue curve at that quantity. At the point of maximum total revenue m the slope of the total revenue curve is zero and the marginal revenue is therefore also zero. The marginal revenue curve thus crosses the horizontal axis at the quantity at which the total revenue is maximum. When the demand curve is a straight line, this occurs at the middle point of the curve, at a point on the horizontal axis that bisects the distance 0 Qm. Past the mid-point of a straight line demand curve, the marginal revenue becomes negative.
Why is marginal revenue important? This question is best answered by way of example. Consider the market for fresh eggs in a locality. Suppose that the government permits producers to establish an Egg Marketing Board with the power to set the price of eggs to the consumer and allocate output quantities to all individual producers. Purchases of eggs from outside the local area are prohibited. This situation is shown in Figure 6. The demand curve is given by the line DD and the supply curve is the horizontal line C0S. A horizontal supply curve is a reasonable assumption here because most of the inputs used to produce eggs can be purchased by egg producers at fixed market prices---these inputs are used by other industries and producers of eggs use a small fraction of the available supply. This implies that chicks can be hatched and raised to hens at constant cost.
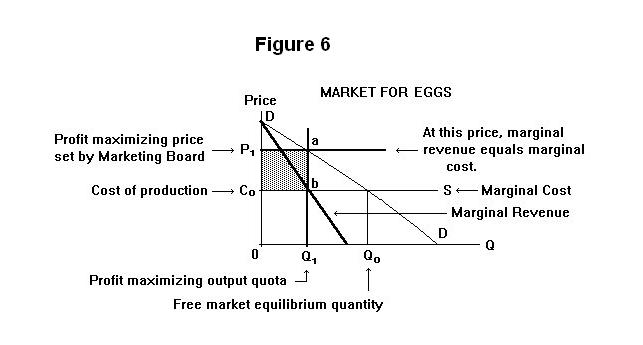
Egg producers like this arrangement because it enables them to sell their eggs to consumers at a price above the cost of production, yielding a profit indicated by the shaded area in Figure 6. The problem faced by the Marketing Board, acting on their behalf, is to determine the quantity level that will maximize that profit. At a lower output quota there is a gain from a higher price, but the quantity producers sell will be less.
The profit is the excess of total revenue, given by the area P1 a Q1 0, over total cost, given by the area C0 b Q10. At every quota level the Board's problem is to decide whether to increase the output quota by one unit. It will do this if the additional revenue from selling another unit to consumers---the marginal revenue---is greater than the additional to total cost from producing another unit---called the marginal cost.
The marginal revenue is given by the thick line in Figure 6. The marginal cost is given simply by the horizontal supply curve---each additional unit produced adds 0 C0 to total cost. Starting from zero, therefore, the Board will increase the quota, unit by unit, until the marginal revenue curve crosses the marginal cost curve (in this case, supply curve). Output will expand until marginal revenue equals marginal cost. At this output level the profit to egg producers will be maximized.
If, starting from the output Q1 in Figure 6, the Board were to increase the output quota by one more unit, the increase in total revenue from selling that unit would be less than the increase in the total cost from producing it, making such an expansion of the quota not worthwhile. Alternatively, if it were to reduce the quota by one unit, the reduction in total revenue from selling one less unit would be greater than the reduction in the total cost from producing one unit less, making the reduction in the quota not worthwhile. Profits are maximized by adjusting the quantity sold to equalize marginal cost and marginal revenue.
Economists have a convention of referring to the elasticity of demand as positive number even though it is in fact negative. When they talk about an elasticity of demand greater than 1 they really mean that the elasticity of demand is less than -1. What they are referring to is the absolute value of the elasticity of demand. The absolute value of -2 is 2, whereas its algebraic value is -2. We obtain a number's absolute value by simply ignoring its sign. So when economists say that the demand is highly elastic they mean that the elasticity is a large number with a negative sign attached.
It is test-time again. Make sure that you think up an answer of your own before looking at the one provided.
Question 1
Question 2
Question 3
Choose Another Topic in the Lesson.