| STCk(y) = | w1y + w2k | if y  k k |
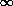 | if y > k. |
TC(y,w1,w2) = w1y + w2y = (w1 + w2)y.Its short run total cost of production when the amount of input 2 is fixed at k is
These functions are shown in the following figure.
STCk(y) = w1y + w2k if y k
if y > k.
Its short run total cost of production when the amount of input 2 is fixed at k is
w1y if w1 < w2 TC(y,w1,w2) = wy if w1 = w2 = w w2y if w1 > w2
Note that in this case if w1 < w2 then there is no level of output for which short run total cost is equal to the long run total cost. In this case the firm would like to use only input 1 to produce any output, so if k > 0 there is no output for which the short run total cost is equal to the long run total cost. The short and long run cost functions in this case are shown in the following figure.
STCk(y) = w2k if y k
w1(y k) + w2k
if y > k.
TC(y,w1,w2) = 2y(w1w2)1/2.
Its short run total cost of production when the amount of input 2 is fixed at k is
STCk(y) =w1y2/k + w2k.Note that TC is a linear function of y while STC is a quadratic function. (Remember that w1 and w2 are fixed.) The functions are shown in the following figure.