The cost function for a firm with two variable inputs

Consider a firm that uses two inputs and has the production function F . This firm minimizes its cost of producing any given output y if it chooses the pair (z1, z2) of inputs to solve the problem
minz1,z2w1z1 + w2z2 subject to y = F (z1, z2),
where w1 and w2 are the input prices. Note that w1, w2, and y are given in this problem---they are parameters. The variables are z1 and z2.

Denote the amounts of the two inputs that solve this problem by z1*(y, w1, w2) and z2*(y, w1, w2). The functions z1* and z2* are the firm's conditional input demand functions. (They are conditional on the output y, which is taken as given.)

The firm's minimal cost of producing the output y is w1z1*(y,w1, w2) + w2z2*(y,w1, w2) (the value of its total cost for the values of z1 and z2 that minimize that cost). The function TC defined by

TC(y,w1,w2) = w1z1*(y,w1, w2) + w2z2*(y,w1, w2)
is called the firm's (total) cost function. (Note that the hard part of the problem is finding the conditional input demands; once you have found these, then finding the cost function is simply a matter of adding the conditional input demands together together with the weights w1 and w2.)

Graphical illustration of the cost-minimization problem

The firm's cost-minimization problem is illustrated in the following figure. The red curve is the y-isoquant: the set of all pairs (z1, z2) of inputs that produce exactly the output y. The light blue area, above the y-isoquant, is the set of all pairs (z1, z2) of inputs that produce at least the output y: the set of feasible input bundles for the output y. Each green line is a set of pairs (z1, z2) of inputs that are equally costly: an isocost line. The points on any given isocost line satisfy the condition
w1z1 + w2z2 = c
for some value of c. Isocost lines further from the origin correspond to higher costs.

The cost-minimization problem of the firm is to choose an input bundle (z1, z2) feasible for the output y that costs as little as possible. In terms of the figure, a cost-minimizing input bundle is a point on the y-isoquant that is on the lowest possible isocost line. Put differently, a cost-minimizing input bundle must satisfy two conditions:

In the figure, there is a single cost-minimizing input bundle, indicated by the black dot.

Another example of a firm's cost-minimization problem is given in the following figure. In this case the isoquant does not have the "typical" convex-to-the-origin shape; instead, it is bowed out from the origin. The cost-minimizing bundle is, as before, the bundle on the isoquant that is on the lowest possible isocost curve. This bundle is indicated by the large black dot. (Note that the point at which an isocost line is tangent to the isoquant maximizes the cost of producing the output y along the isoquant.)

The case of smooth isoquants convex to the origin

If the y-isoquant is smooth and the cost-minimizing bundle involves a positive amount of each input, as in the first figure, we can see that at a cost-minimizing input bundle an isocost line is tangent to the y-isoquant.

Now, the equation of an isocost line is

w1z1 + w2z2 = c
which we can rewrite as
z2 = c/w2 (w1/w2)z1
so that we see that is slope is 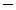w1/w2. The absolute value of the slope of an isoquant is the MRTS, so we reach the following conclusion.
If the isoquants are smooth and convex to the origin and the cost-minimizing input bundle (z1, z2) involves a positive amount of each input, then this bundle satisfies the following two conditions:

The condition that the MRTS be equal to w1/w2 can be given the following intuitive interpretation. We know that the MRTS is equal to MP1/MP2. So the condition that the MRTS be equal to w1/w2 is equivalent to the condition

w1/w2 = MP1/MP2,
or
MP1/w1 = MP2/w2:
the marginal product per dollar is equal for the two inputs. That is, the condition that MRTS be equal to w1/w2 is equivalent to the condition that at a cost minimizing bundle, a dollar spent on each input must yield the same marginal output. This condition makes sense: if a dollar spent on input 1 yields more output than a dollar spent on input 2, then more of input 1 should be used and less of input 2. Only if a dollar spent on each input is equally productive is the input bundle optimal.

Examples and exercises for cost-minimization problems

Copyright © 1997 by Martin J. Osborne